Hierarchical Modeling of Song Sparrows

Linear mixed-effects models with time correlation for analyzing avian reproduction.

Table of Contents

Introduction

Find the detailed github repository here.

Understanding the factors that drive reproductive success in birds offers valuable insights into ecological and evolutionary processes. For song sparrows, reproductive variability may stem from a combination of individual traits—such as fitness, age, or nesting behavior—and environmental influences like competition and nesting site quality.

To explore these dynamics, a multiyear observational study was conducted on a population of song sparrows inhabiting an island in the Pacific Northwest. Known for their monogamous behavior during mating seasons and strong territorial instincts, these sparrows exhibit fascinating patterns: females typically establish their first nests at one year old and remain loyal to suboptimal nesting sites year after year.

This analysis seeks to uncover the ecological and biological drivers of reproductive variability in this population. Specifically, it addresses the following key questions:

  • How do individual-level factors, such as age or nesting location, and population-level variables, such as competition (population density), influence reproductive success?

  • Are there observable trends or patterns in reproductive success across different years or cohorts of sparrows?

  • How do individual characteristics and environmental factors interact to influence variability in reproductive outcomes?

Key Insights

This analysis applies a linear mixed-effects model to investigate the factors influencing reproductive success in song sparrows. The model includes fixed effects for population density, nesting location, and age, as well as a random intercept to capture differences between years. Additionally, an AR(1) correlation structure is used to account for patterns over time. The key findings are:

  • Population density and nesting location have a significant impact on reproductive success.

  • Age does not show a statistically significant effect on reproduction.

  • Year-to-year differences are effectively captured by the random intercept and the AR(1) structure, highlighting the importance of accounting for temporal variability.

These findings emphasize the value of including both fixed and random effects in ecological models. Future work could explore non-linear relationships and incorporate additional ecological variables to provide a more comprehensive understanding of reproductive success.

Methods Overview

  • Study Design: Provide a detailed description of the study design, including information on sample size(s), macro and micro explanatory variables, and any other relevant features of how the data were gathered.

  • Data description:

    • Handle missingness and correlation between variables.

    • Use visualizations to describe the main sources of heterogeneity in the dataset, such as grouping factors and explanatory variables.

    • Conduct preliminary modeling by performing sequential hypothesis testing on models with micro variables, macro variables, followed by models with interaction terms, using outputs from ANOVAs.

  • Model fitting and diagnostics: Develop a hierarchical model (Linear Mixed-Effects Model) for the dataset that includes explanatory variables and grouping factors. Next, model the temporal correlation using an autoregressive structure. Use model selection criteria to compare this model to other models and choose one that describes all major sources of variation in the dataset. Evaluate any modeling assumptions.

Comparison of models based on their specifications and BIC values

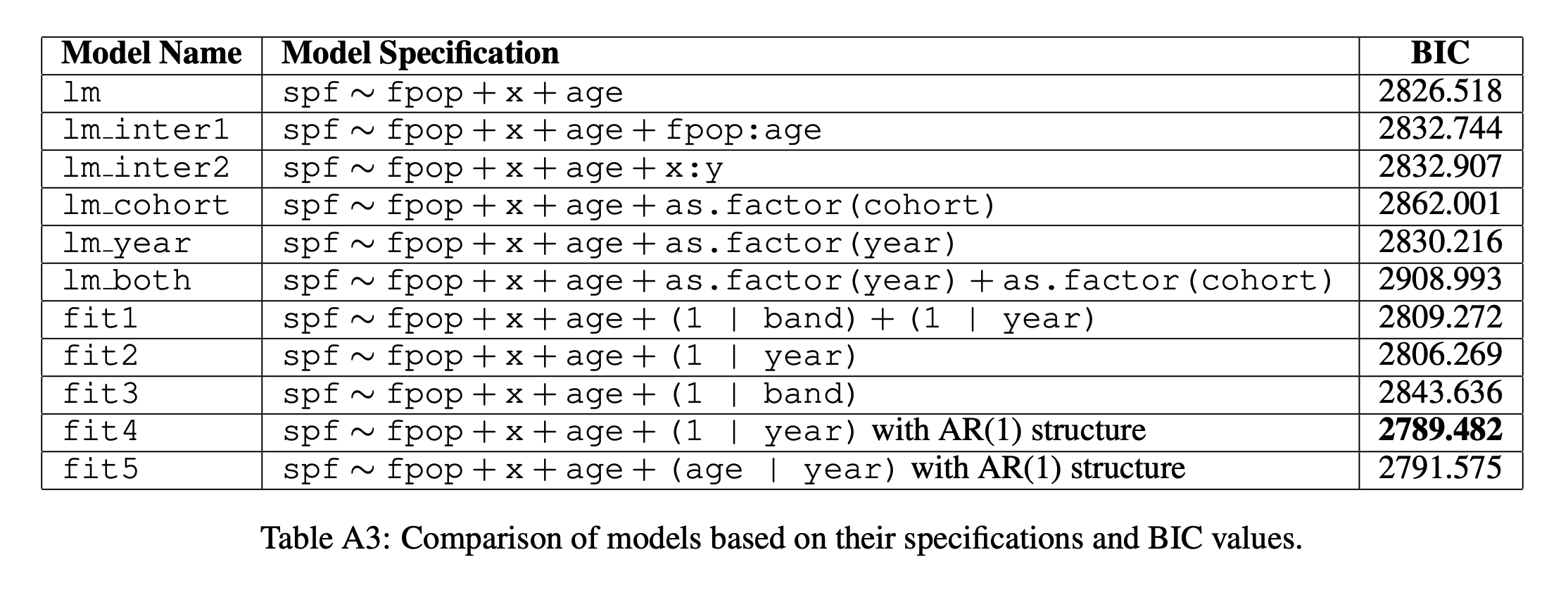
  • Model and data analysis interpretation: Based on the final model, interpret fixed effects parameters, including confidence intervals for continuous or binary explanatory variables, and across-level comparisons for categorical factor variables. Use the results of the model fitting and data analysis to report findings related to the primary question of interest.

  • Conclusions: Describe the scientific conclusions of the data analysis, including a qualitative, non-numerical summary of the hypothesis tests, model selection, and parameter estimates.

Full Report

Find all the details in the full project report below:

It appears you don't have a PDF plugin for this browser. You can click here to download the PDF file.

Acknowledgement

This report is a direct application of knowledge from my STA 610 course on hierarchical models, taught by Professor Peter Hoff.